RWA#1: Unit M Concept 5 - Conic Sections in Real Life (Parabola)

1. Definition: The set of all points that are equal distance from a point (focus) and a line (directrix)

https://people.richland.edu/james/lecture/m116/conics/paradef.html

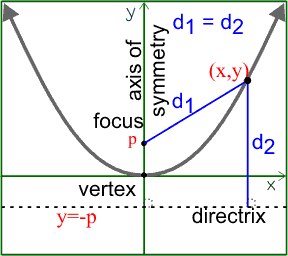
2. Algebraically, the standard equation is (x-h)^2=4p(y-k) or (y-k)^2=4p(x-h), depending if the graph goes right, left, up, or down. The parabola will go up if x appears first and p is positive. It will go down if x appears first and p is negative. It will go right if y is first and p is positive, and left is when y appears first and p is negative. Your vertex is (h,k) and the directrix is a dotted line that is p units away from the vertex, in the opposite direction of the focus. The axis of symmetry will be perpendicular to the directrix and it will always go through the vertex and the focus. In addition, you don't have to find the eccentricity because it is always be equal to one. 

    Graphically, the parabola goes in four directions depending on the x and y, as mentioned above. The vertex is in between the focus and directrix (FVD or DVF). The focus will always be on the inside of the parabola. As seen on the picture above, the point from the focus to a point on the parabola to the directrix will be the same distance.

Here's a cool video to learn more on parabolas: This video will show you that there are parabolas in video games such as Mario. It shows how the parabola would become skinnier/fatter if he ran while jumping or jumped normally.

3. Real World Application: Not only does parabolas appear in video games (shown in the video above), but they also appear on bridges, roller coasters, and satellite dishes. The picture displayed below is a Roman aqueduct, it would help channel water and was a major component in the Roman water supply. A more sophisticated example would be the satellite dishes. The structure of the dish enables it to transmit and detect signals from a specific source. When the signal bounces off of the dish it creates a parabola.

http://someinterestingfacts.net/how-roman-aqueducts-were-made/

http://img.ehowcdn.com/article-new-thumbnail/ds-photo/getty/article/163/99/78431210.jpg

4. Work Cited:
https://people.richland.edu/james/lecture/m116/conics/paradef.html
http://www.youtube.com/watch?v=E_0AHIaK48A
http://someinterestingfacts.net/how-roman-aqueducts-were-made/
http://img.ehowcdn.com/article-new-thumbnail/ds-photo/getty/article/163/99/78431210.jpg